(Huang et al., 2018) at ICLR

Ah, phrase-based machine translation. Translating spans of words, rather than individuals. It harkens back to a quainter time, before the neural craze. And now, it seems that we’re marrying it to the neural craze. On some simple experiments, the model (a venture by Microsoft Research) outperforms an NMT baseline and gives outputs that humans like, too.

One of my favorite tongue-in-cheek papers shows how we are dependent on phrases to represent concepts. It opposes a notion of epistemic parsimony—if it’s truly a freestanding concept, doesn’t it deserve its own word? Our lexicon, nonetheless, includes these phrases. They have their own (often non-compositional) meanings, so it makes sense to treat them as units.

To let neural machine translation (NMT) handle these, the authors build on “sleep–wake networks” (SWAN), which unfortunately assume monotonic alignments between inputs and outputs—no reordering. Reordering is common between language pairs, so the authors introduce a soft local reordering of the input.

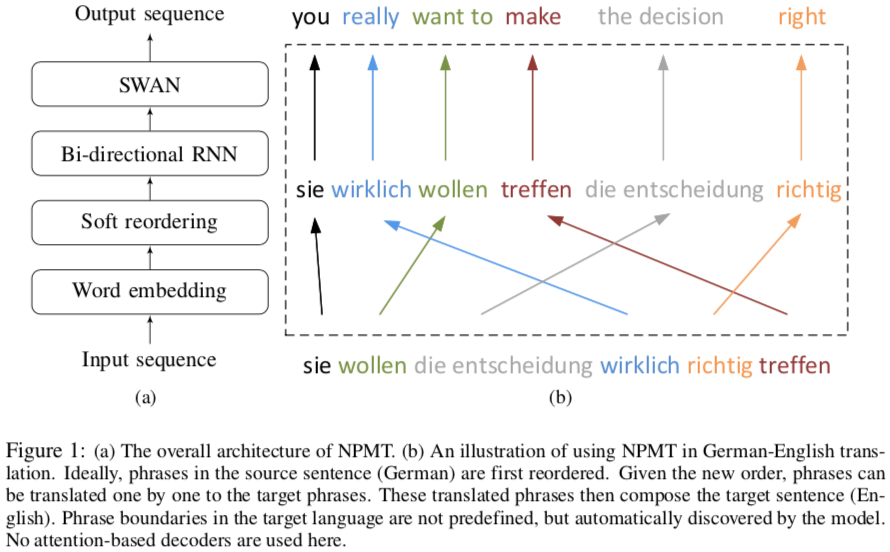
Although prior work has identified phrases, e.g. by SMT systems, this work finds phrases automatically from the training data, without attention—perhaps attention isn’t all you need.

Let’s look at what their SWAN model is. The input sequence x (the outputs of the encoder, not the source sentence) has elements 1:T’, and the output sequence y has elements 1:T. There exists as set S_y of valid segmentations of y. The number of segments in each segmentation equals the input sequence length T’. (Sometimes the target sentence is shorter than the source. You’d need null segments to allow this, which balloons the complexity—good thing we marginalize this out.) The probability of a sequence is the marginal probability of the sequence given the input sequence—you marginalize over all possible segmentations. This eliminates them, a latent variable, from your consideration.

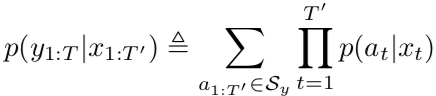
SWAN gives the probability of a segment given a token using a softmax layer, creating a distribution over all possible segments.

The generative model is:

segments = []
for t in range(1, T' + 1):
	x_t = x[t]
	segment = []
	while True:
		rnn = RNN(x_t)
		sample = next(rnn)
		if sample == "$":  # end of segment symbol
			break
		else:
			segment.append(sample)
	segments.append(segment)
y = concatenate(segments)

The big trick here is the same as what’s used in CKY parsing. There are an exponential number of segmentations: each inter-word gap can either start or not start a new segment. But there are only a quadratic number of segments: each is defined by only a starting and ending index.

With this in place, and using the RNN-to-softmax, we can sample a segment for each input token in parallel, then concatenate these. This is non-autoregressive, which eliminates a major bottleneck in neural MT. (They do reintroduce the normal bottleneck, though, because they’re using an RNN, which can’t be trained in parallel.)