(Borovykh, Bohte, and Oosterlee, 2017) on arXiv

Convolutional networks are nice for sequence prediction, because the computations can be parallelized, unlike in recurrent networks. (I’ve previously given a cutesy demo of how the convolutional filter slides over the input.) Evidently these can be used for time series forecasting, and it looks a lot like neural language modeling.

Their task is to predict the next value in a time series, conditioned on its predecessors. This is identical to language modeling, except that the domain is continuous (real numbers) instead of discrete (some vocabulary of words). It’s a simple enough architectural change: replace the softmax layer at the end (which returns a probability distribution) with a great big nothing. Just train the raw values to predict your real-valued result.

No, that’s not the big architectural improvement. The cleverness comes from dilated convolutions: convolutions on convolutions on convolutions, so longer-term dependencies can be captured. All this is doable with very few parameters—you reuse the convolutional kernel.

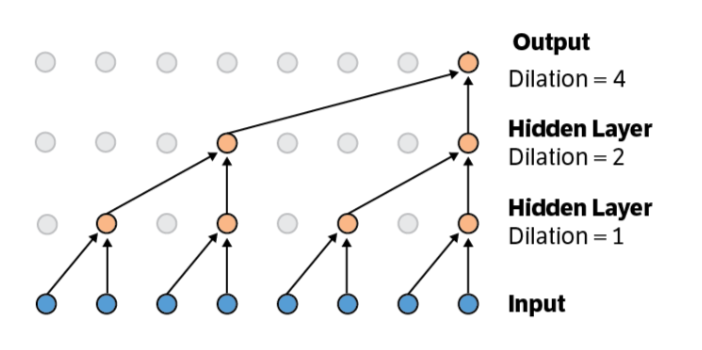
You can also predict arbitrarily far into the future, but your errors will propagate: feed the output of your network back in until you’ve stepped far enough forward to predict at the time of interest.

The author strain to minimize mean absolute error, and they employ an L2 penalty on the weights as regularization. They use ReLU as their nonlinearity. They also use highway connections to feed values up to higher layers in the network. The justification is that if the correct mapping to learn is close to the identity function, you waste effort and may not even find it without these connections.

They compare their model to an LSTM, but I have the sinking suspicion that the LSTM has fewer parameters, so it’s bound to be less expressive. Still, their model has the lowest squared error consistently, giving the other models a run for their money.